Pada materi grafik fungsi kuadrat telah disinggung bahwa jika digambarkan pada bidang koordinat, grafik fungsi kuadrat akan berbentuk sebuah parabola dengan karakteristik tergantung dari koefisien-koefisien fungsi kuadrat tersebut.
Berikut beberapa karakteristik yang perlu diperhatikan dalam mensketsa grafik fungsi kuadrat.
1. a > 0 : parabola terbuka ke atas
2. a < 0 : parabola terbuka ke bawah
3. D > 0 : memotong sumbu-x di dua titik
4. D = 0 : menyinggung sumbu-x
5. D < 0 : tidak memotong sumbu-x
Dari karakteristik diatas, kita akan memperoleh gambaran kasar tentang grafik fungsi kuadrat tersebut, yang tentu saja akan memudahkan dalam mensketsa nantinya.
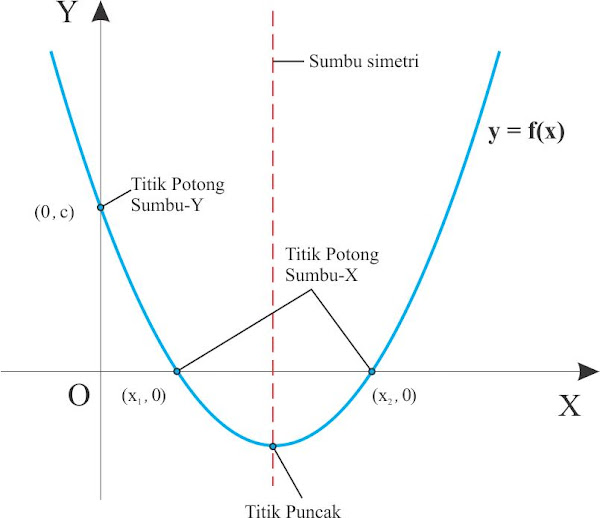
Unsur-unsur grafik fungsi kuadrat
Diberikan fungsi kuadrat \(\mathrm{y=f(x)=ax^{2}+bx+c}\)
1. Titik potong sumbu-X
y = f(0) = a(0)2 + b(0) + c = c $$\mathrm{\left ( 0,c \right )}$$
Catatan :
- Jika D = 0, maka titik potong sumbu-x dan titik puncak berada pada titik yang sama, sehingga cukup dicari salah satunya saja.
- Jika D < 0, grafik tidak mempunyai titik potong sumbu-x.
- Jika b = 0, maka titik potong sumbu-y dan titik puncak berada pada titik yang sama, sehingga cukup dicari salah satunya saja.
Contoh 1
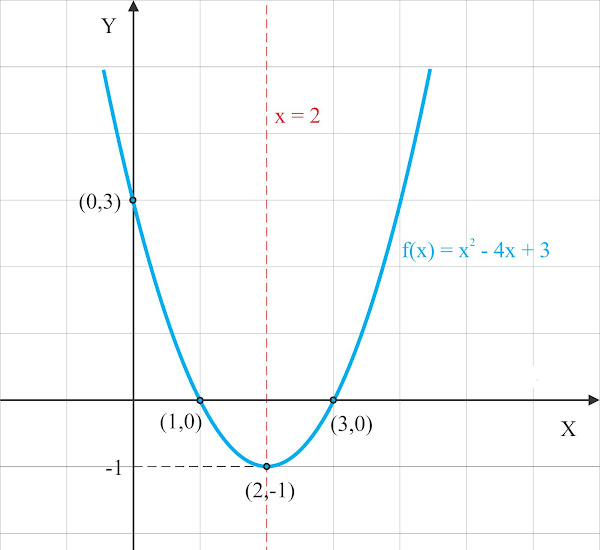
Sketsalah grafik fungsi kuadrat \(\mathrm{f(x)=x^{2}-4x+3}\)
Jawab :
a = 1 > 0 (parabola terbuka ke atas)
b = −4
c = 3
D = b2 − 4ac
D = (−4)2 − 4.1.3 = 4
D = 4
Karena D > 0, maka parabola memotong sumbu-x di dua titik.
Titik potong sumbu-x ⇒ y = 0
x2 − 4x + 3 = 0
(x − 1)(x − 3) = 0
x = 1 atau x = 3
⇒ (1, 0) dan (3, 0)
Titik potong sumbu-y ⇒ x = 0
(0, c) ⇒ (0, 3)
Persamaan sumbu simetri
x = \(\mathrm{\frac{-b}{2a}}\) = \(\mathrm{\frac{-(-4)}{2.1}}\) = 2
x = 2
Nilai ekstrim
y = \(\mathrm{\frac{-D}{4a}}\) = \(\mathrm{\frac{-4}{4.1}}\) = −1
y = −1
Titik puncak
\(\mathrm{P\left ( \frac{-b}{2a},\frac{-D}{4a} \right )}\) ⇒ (2, −1)
Lukis titik-titik yang diperoleh pada bidang koordinat, kemudian hubungkan sehingga membentuk sebuah parabola.
Contoh 2
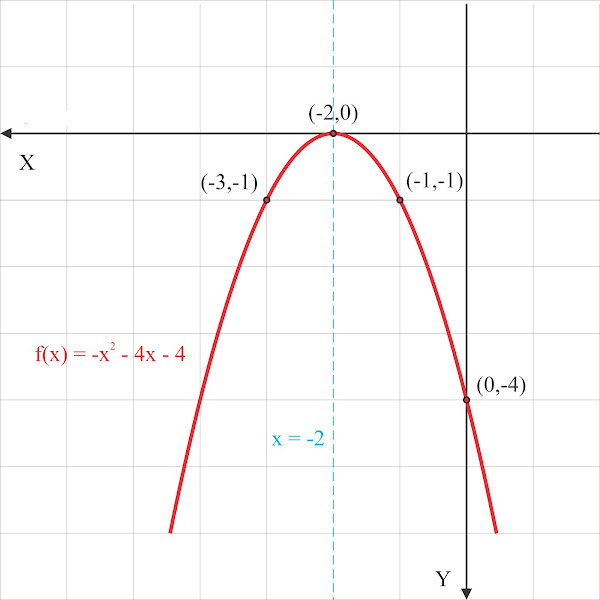
Gambarlah grafik fungsi kuadrat \(\mathrm{f(x)=-x^{2}-4x-4}\)
Jawab :
a = −1 < 0 (parabola terbuka ke bawah)
b = −4
c = −4
D = b2 − 4ac
D = (−4)2 − 4.(−1).(−4)
D = 0
Karena D = 0, maka parabola menyinggung sumbu-x, menyebabkan titik potong sumbu-x dan titik puncak berada pada titik yang sama.
Titik potong sumbu-x ⇒ y = 0
−x2 − 4x − 4 = 0
x2 + 4x + 4 = 0
(x + 2)(x + 2) = 0
x = −2
⇒ (−2, 0)
Karena titik potong sumbu-x dan titik puncak sama, yaitu (−2, 0), maka diperoleh :
Persamaan sumbu simetri : x = −2
Nilai ekstrim : y = 0
Titik potong sumbu-y ⇒ x = 0
(0, c) ⇒ (0, −4)
Karena untuk menggambar parabola minimal diperlukan tiga buah titik, untuk itu kita dapat menentukan titik-titik bantu disekitar sumbu simetri (x = −2).
Untuk x = −1
y = f(−1) = −(−1)2 − 4(−1) − 4 = −1
⇒ (−1, −1)
Untuk x = −3
y = f(−3) = −(−3)2 − 4(−3) − 4 = −1
⇒ (−3, −1)
Lukis titik-titik yang diperoleh pada bidang koordinat, kemudian hubungkan sehingga membentuk sebuah parabola.
Contoh 3
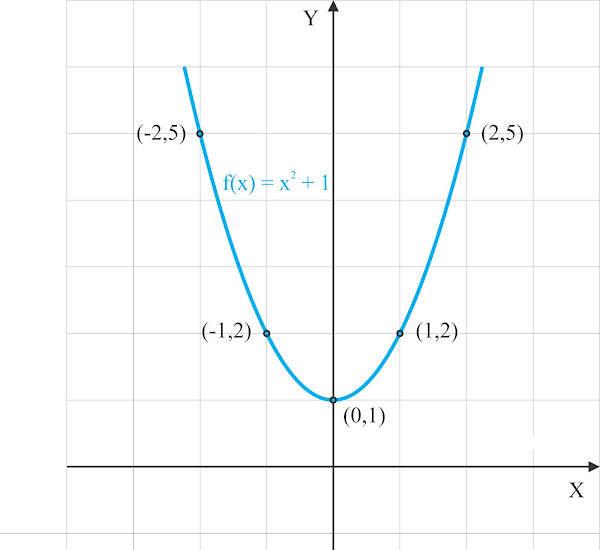
Gambarlah grafik fungsi kuadrat \(\mathrm{f(x)=x^{2}+1}\)
Jawab :
a = 1 > 0 (parabola terbuka ke atas)
b = 0 (titik potong sumbu-y = titik puncak)
c = 1
D = b2 − 4ac
D = (0)2 − 4.1.1\
D = −4
Karena D < 0 maka parabola tidak mempunyai titik potong sumbu-x.
Titik potong sumbu-y
(0, c) ⇒ (0, 1)
Karena titik potong sumbu-y dan titik puncak sama yaitu : (0, 1), maka diperoleh :
Persamaan sumbu simetri : x = 0
Nilai ekstrim : y = 1
Titik-titik bantu :
Untuk x = 1
y = f(1) = (1)2 + 1 = 2
⇒ (1, 2)
Untuk x = 2
y = f(2) = (2)2 + 1 = 5
⇒ (2, 5)
Untuk x = −1
y = f(−1) = (−1)2 + 1 = 2
⇒ (−1, 2)
Untuk x = −2
y = f(−2) = (−2)2 + 1 = 5
⇒ (−2, 5)
Catatan :
Dengan mencerminkan titik-titik (1, 2) dan (2, 5) ke sumbu simetri (x = 0), maka akan diperoleh titik-titik (−1, 2) dan (−2, 5). Jadi tidak harus dicari satu per satu seperti cara diatas.
Selanjutnya, dengan menghubungkan titik-titik yang diperoleh pada bidang koordinat, maka akan terbentuk sebuah parabola sebagai berikut :
Grafik fungsi diatas merupakan salah satu contoh grafik fungsi definit positif, dimana grafiknya tidak memotong sumbu-x dan untuk setiap nilai x, grafiknya selalu berada diatas sumbu-x.