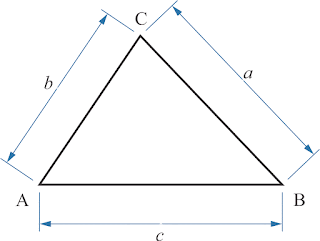
Perkalian titik (dot product) dari dua vektor a dan b dinotasikan dengan a ‧ b.
Perkalian titik disini tidak sama dengan perkalian aljabar seperti yang sudah kita kenal, karena yang dilibatkan disini adalah vektor, bukan bilangan.
Diberikan dua buah vektor,
a = [a1 , a2 , a3]
b = [b1 , b2 , b3]
dengan θ adalah sudut antara a dan b, seperti yang terlihat pada gambar.
Dengan bantuan aturan cosinus, kita peroleh
|b – a|2 = |a|2 + |b|2 – 2|a| |b| cos θ
|a| |b| cos θ = \(\frac{1}{2}\)( |a|2 + |b|2 – |b – a|2 ) (*)
Substitusikan
|a|2 = a12 + a22 + a32 ,
|b|2 = b12 + b22 + b32 ,
|b – a|2 = (b1 – a1)2 + (b2 – a2)2 + (b3 – a3)2,
pada ruas kanan persamaan (*), lalu sederhanakan hingga diperoleh
Persamaan terakhir ini cukup menarik, karena mampu menjelaskan hubungan antara panjang, sudut, dan komponen-komponen suatu vektor secara bersamaan.
Persamaan yang didominasi oleh operasi perkalian inilah yang kemudian menjadi ide dalam pendefinisian perkalian titik dua vektor.
Definisi
Misalkan a dan b adalah vektor-vektor bukan nol. Perkalian titik atau dot product dari a dan b, ditulis a ‧ b, didefinisikan
dimana
|a| = panjang a
|b| = panjang b
θ = sudut antara a dan b
Dengan demikian, persamaan (**) dapat ditulis menjadi
Perkalian titik dari dua vektor akan menghasilkan skalar. Oleh sebab itu, perkalian titik sering disebut dengan perkalian skalar (skalar product).
Contoh 1
Dua buah vektor u dan v membentuk sudut sebesar 60°. Jika |u| = 4 dan |v| = 7, maka u ‧ v = …
Jawab :
u ‧ v = |u| |v| cos 60°
u ‧ v = 4 ‧ 7 ‧ \(\frac{1}{2}\)
u ‧ v = 14
Contoh 2
Diketahui p dan q adalah vektor-vektor di R3, dengan p = 2i – 3j + 4k dan q = 3i – k. Tentukan nilai p ‧ q
Jawab :
p = [2 , -3 , 4]
q = [3 , 0 , -1]
p ‧ q = 2 ‧ 3 + (-3) 0 + 4 (-1)
p ‧ q = 6 + 0 – 4
p ‧ q = 2
Contoh 3
Diketahui p = [6 , 0] dan q = [4 , -4]. Tentukan besar sudut yang dibentuk oleh p dan q !
Jawab :
Panjang masing-masing vektor :
|p| = √(62 + 02) = 6
|q| = √(42 + (-4)2) = 4√2
Hasil kali titik dari kedua vektor :
p ‧ q = 6 ‧ 4 + 0 (-4) = 24
Misalkan sudut diantara p dan q adalah θ.
\(\begin{align}
\mathrm{cos\,\theta} =\frac{\mathbf{p}\cdot \mathbf{q}}{\mathbf{|p||q|}}=\frac{24}{6\cdot 4\sqrt{2}}=\frac{1}{2}\sqrt{2}
\end{align}\)
Karena cos θ = \(\frac{1}{2}\)√2, maka θ = 45°
Sifat-Sifat Perkalian Titik
Jika a, b dan c adalah vektor, dan k adalah skalar/bilangan, maka
- a ‧ a = |a|2
- a ‧ b = b ‧ a
- a ‧ (b + c) = a ‧ b + a ‧ c
- a ‧ (kb) = k(a ‧ b) = (ka) ‧ b
- Dua vektor yang saling tegak lurus membentuk sudut sebesar 90°
- Dua vektor yang searah membentuk sudut sebesar 0°
- Dua vektor yang berlawanan arah membentuk sudut sebesar 180°
- Ketika θ lancip, maka cos θ > 0
- Ketika θ tumpul, maka cos θ < 0
Jika a berlawanan arah dengan b, maka
a ‧ b = -|a| |b|
Jika θ lancip (0 < θ < 90°), maka
a ‧ b > 0
Jika θ tumpul (90° < θ < 180°), maka
a ‧ b < 0
Contoh 4
Diketahui u = [3 , 1 , -2] dan v = [4 , 0 , k]. Tentukan k agar kedua vektor tersebut saling tegak lurus.
Jawab :
Agar u tegak lurus v, haruslah u ‧ v = 0
\(\begin{align}
\mathbf{u\cdot v} &=0 \\
3\cdot 4+1\cdot 0+(-2)k&=0 \\
12-2k&=0 \\
12 &=2k \\
k&=6
\end{align}\)
Jika u = [u1 , u2], tunjukkan bahwa u ‧ u = |u|2
Jawab :
Berdasarkan definisi perkalian titik, maka
Panjang dari Jumlah atau Selisih Dua Vektor
Diberikan dua vektor a dan b, dengan θ adalah sudut antara vektor a dan b. Jika c = a + b, maka
c ‧ c = (a + b) ‧ (a + b)
c ‧ c = a ‧ a + b ‧ b + 2 a ‧ b
Karena c ‧ c = |c|2 , a ‧ a = |a|2 , dan b ‧ b = |b|2 , persamaan diatas menjadi
|c|2 = |a|2 + |b|2 + 2 a ‧ b
Jika kita substitusikan kembali c = a + b, maka akan kita peroleh
Karena a ‧ b = |a| |b| cos θ, persamaan diatas dapat pula ditulis menjadi
Dengan cara yang sama, untuk c = a – b, akan diperoleh
atau
Uraian-uraian diatas, dapat pula kita tuliskan sebagai berikut.
1. Jika c = a + b, maka berlaku
2. Jika c = a – b, maka berlaku
dimana |a|, |b| dan |c| berturut-turut adalah panjang dari vektor a, b dan c.
Contoh 5
Diketahui |a| = 5, |b| = 3 dan |a – b| = 2√6. Apabila a dan b membentuk sudut lancip sebesar α, tentukan nilai sin α
Jawab :
|a – b|2 = |a|2 + |b|2 – 2 |a| |b| cos α
(2√6)2 = (5)2 + (3)2 – 2 (5) (3) cos α
24 = 34 – 30 cos α
30 cos α = 10
cos α = \(\frac{1}{3}\) ⟶ sin α = \(\frac{2}{3}\)√2
Contoh 6
Diketahui |a| = 2√2, |b| = 10 dan a ‧ b = 4. Apabila a = b – c, maka a ‧ c = …
Jawab :
Karena a = b – c, maka c = b – a. Akibatnya
|c|2 = |b|2 + |a|2 – 2 b ‧ a
|c|2 = (10)2 + (2√2)2 – 2 (4)
|c|2 = 100
|c| = 10
Karena a = b – c, maka b = a + c. Akibatnya
|b|2 = |a|2 + |c|2 – 2 a ‧ c
(10)2 = (2√2)2 + (10)2 + 2 a ‧ c
2 a ‧ c = -8
a ‧ c = -4
Soal Latihan dan Pembahasan
Latihan 1
Diketahui tiga buah titik A(2, -4, -2), B(3, -4, -1) dan C(4, -3, -1). Jika p dan q berturut-turut adalah wakil dari vektor AB dan BC, tentukan besar sudut yang dibentuk oleh p dan q.
Jawab :
AB = [3, -4, -1] – [2, -4, -2]
AB = [1, 0, 1]
BC = [4, -3, -1] – [3, -4, -1]
BC = [1, 1, 0]
Diperoleh
p = AB = [1, 0, 1]
q = BC = [1, 1, 0]
Misalkan sudut antara p dan q adalah α.
\(\begin{align}
\mathrm{Cos\,\alpha} &=\frac{\mathbf{p}\cdot \mathbf{q}}{\mathbf{|p|\,|q|}} \\
&=\frac{1\cdot 1+0\cdot 1+1\cdot 0}{\sqrt{1^{2}+0^{2}+1^{2}}\cdot \sqrt{1^{2}+1^{2}+0^{2}}} \\
&=\frac{1}{2}
\end{align}\)
Karena cos α = 1/2, maka α = 60°
Latihan 2
Diketahui |a| = 3, |b| = 5 dan |a + b| = 2√13 . Tentukan |a – b|
Jawab :
|a + b|2 = |a|2 + |b|2 + 2 a ‧ b
(2√13)2 = (3)2 + (5)2 + 2 a ‧ b
52 = 9 + 25 + 2 a ‧ b
2 a ‧ b = 18
|a – b|2 = |a|2 + |b|2 – 2 a ‧ b
|a – b|2 = (3)2 + (5)2 – 18
|a – b|2 = 16
|a – b| = 4
Latihan 3
Diketahui tiga vektor u, v dan w, dengan |u| = 4 , |w| = √13 dan u ‧ v = 6. Jika v = u + w dan sudut antara v dan w adalah β, maka sin2β = …
Jawab :
Karena v = u + w, maka w = v – u . Akibatnya
|w|2 = |v|2 + |u|2 – 2 v ‧ u
(√13)2 = |v|2 + (4)2 – 2 (6)
13 = |v|2 + 4
|v|2 = 9
|v| = 3
Karena v = u + w, maka u = v – w . Akibatnya
|u|2 = |v|2 + |w|2 – 2 v ‧ w
(4)2 = (3)2 + (√13)2 – 2 v ‧ w
2 v ‧ w = 6
v ‧ w = 3
Sudut antara v dan w adalah β, sehingga
\(\begin{align}
\mathrm{cos}\,\beta =\mathbf{\frac{v\cdot w}{\left | v \right |\,\left | w \right |}}=\frac{3}{3\cdot \sqrt{13}}=\frac{1}{\sqrt{13}}
\end{align}\)
Berdasarkan identitas phythagoras :
\(\begin{align}
sin^{2}\beta &=1-cos^{2}\beta \\
& = 1-\left ( \frac{1}{\sqrt{13}} \right )^{2} \\
& = 1-\frac{1}{13} \\
& = \frac{12}{13}
\end{align}\)
Latihan 4
Dari suatu segitiga sama sisi ABC diketahui A(2, -1) dan B(4, 1). Tentukan koordinat titik C yang mungkin
Jawab :
Misalkan koordinat titik C adalah (x, y)
AB = [4, 1] – [2, -1] = [2, 2]
AC = [x, y] – [2, -1] = [x – 2 , y + 1]
Panjang AB dan AC berturut-turut :
|AB| = √(22 + 22) = √8
|AC| = √((x – 2)2 + (y + 1)2) = √(x2 + y2 – 4x + 2y + 5)
Karena ABC sama sisi, maka |AC| = |AB|.
√(x2 + y2 – 4x + 2y + 5) = √8
x2 + y2 – 4x + 2y + 5 = 8
x2 + y2 – 4x + 2y – 3 = 0 ……………………………..(1)
Karena AB = [2, 2] dan AC = [x – 2, y + 1] maka
AB ‧ AC = 2(x – 2) + 2(y + 1)
AB ‧ AC = 2x – 4 + 2y + 2
AB ‧ AC = 2x + 2y – 2 ………………………………..(2)
Karena ABC sama sisi, maka sudut antara AB dan AC adalah 60°. Akibatnya,
AB ‧ AC = |AB| |AC| cos 60°
AB ‧ AC = √8 √8 \(\frac{1}{2}\)
AB ‧ AC = 4 ………………………………………………..(3)
Dari persamaan (2) dan (3) diperoleh hubungan
2x + 2y – 2 = 4
2x + 2y = 6
x + y = 3
y = 3 – x …………………………………………………….(4)
Subsitusi persamaan (4) ke persamaan (1)
x2 + (3 – x)2 – 4x + 2(3 – x) – 3 = 0
x2 + 9 – 6x + x2 – 4x + 6 – 2x – 3 = 0
2x2 – 12x + 12 = 0
x2 – 6x + 6 = 0
Dengan menggunakan rumus kuadrat diperoleh
x = 3 + √3 atau x = 3 – √3
Substitusikan nilai -nilai x ke persamaan (4) :
Untuk x = 3 + √3 → y = -√3
Untuk x = 3 – √3 → y = √3
Jadi, koordinat titik C yang mungkin adalah
C(3 + √3 , -√3) atau C(3 – √3 , √3)