Menentukan Nilai Stasioner dan Jenis Ekstrim Fungsi Pada Matematika

Nilai stasioner : f(2) = (2)2 − 4(2) = −4
Titik stasioner : (2, −4)

Contoh 2
Tentukan nilai stasioner dan titik stasioner dari fungsi \(\mathrm{f(x)=x^{3}-3x+1}\)
Jawab :
f ‘(x) = 3×2 − 3

Nilai stasioner pada x = 1 :
f(1) = (1)3 − 3(1) + 1 = −1

Titik stasioner : (−1, 3) dan (1, −1)

Nilai-nilai stasioner sering juga disebut sebagai bakal calon nilai ektrim. Ada 2 jenis ektrim fungsi, yaitu nilai balik maksimum dan nilai balik minimum. Nilai balik maksimum/minimum sering juga disebut dengan nilai maksimum/minimum relatif atau maksimum/minimum lokal.

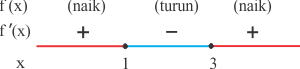
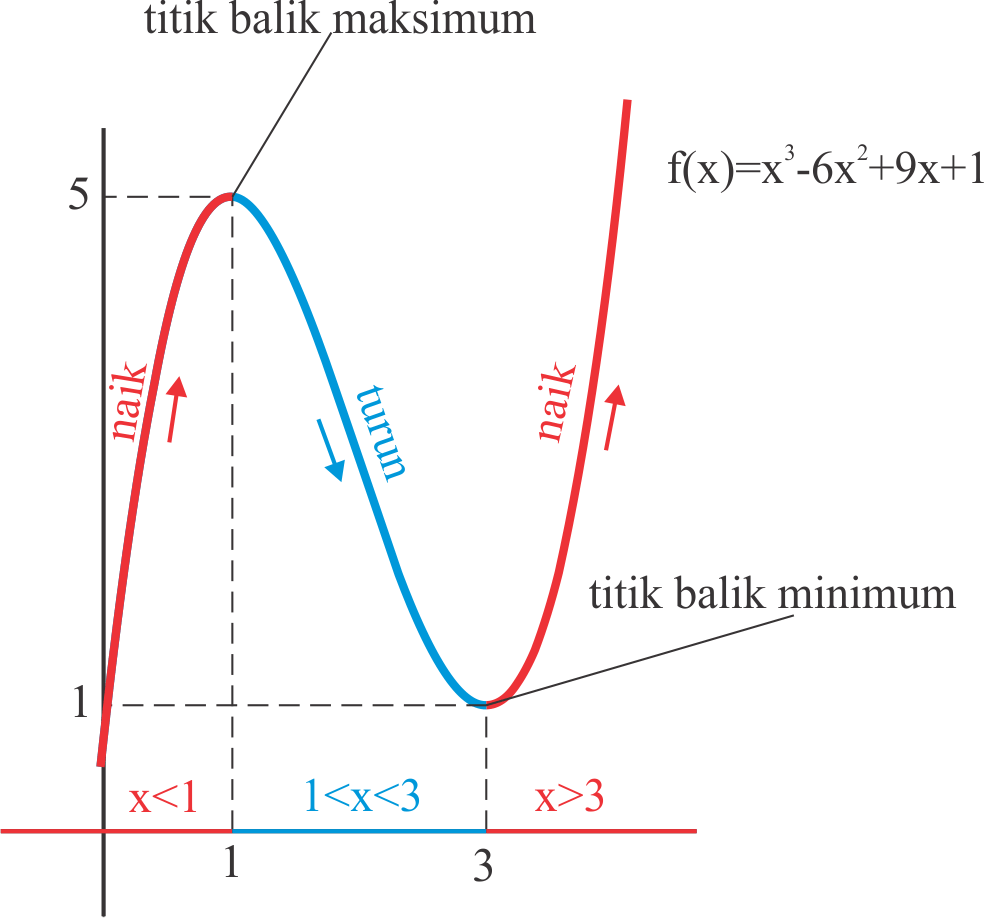
Untuk menentukan jenis ektrim suatu fungsi dapat dilakukan dengan uji turunan pertama dan uji turunan kedua.

Contoh 3

Dengan menggunakan uji turunan pertama, tentukan jenis ekstrim dari fungsi \(\mathrm{f(x)=x^{3}-6x^{2}+9x+1}\)

Jawab :

f ‘(x) = 3x² − 12x + 9

f ‘(x) = 0

⇔ 3x² − 12x + 9 = 0

⇔ x² − 4x + 3 = 0

⇔ (x − 1)(x − 3) = 0

⇔ x = 1 atau x = 3

Nilai stasioner di x = 1 adalah

f(1) = (1)³ − 6(1)² + 9(1) + 1 = 5

Nilai stasioner di x = 3 adalah

f(3) =  (3)³ − 6(3)² + 9(3) + 1 = 1

Karena pada x = 1 terjadi perubahan dari naik menjadi turun, maka f(1) = 5 adalah nilai balik maksimum.

Karena pada x = 3 terjadi perubahan dari turun menjadi naik, maka f(3) = 1 adalah nilai balik minimum.

Sketsa grafik (update 18/5/17)

Uji Turunan Kedua

Misalkan f(a) adalah nilai stasioner di x = a

• Jika f ”(a) < 0 maka f(a) adalah nilai balik maksimum. 
• Jika f ”(a) > 0 maka f(a) adalah nilai balik minimum. 
• Jika f ”(a) = 0 maka jenis ekstrim belum dapat ditetapkan (gunakan uji turunan pertama untuk menentukan jenis ekstrimnya)

Contoh 4

Dengan menggunakan uji turunan kedua, tentukan jenis ekstrim dari fungsi \(\mathrm{f(x)=x^{3}-6x^{2}+9x+1}\)

Jawab :

f ‘(x) =  3x² − 12x + 9

f ”(x) = 6x − 12

f ‘(x) = 0

⇔ 3x² − 12x + 9 = 0

⇔ x² − 4x + 3 = 0

⇔ (x − 1)(x – 3) = 0

⇔ x = 1 atau x = 3

Nilai stasioner pada x = 1 :

f(1) = (1)³ − 6(1)² + 9(1) + 1 = 5

Nilai stasioner pada x = 3

f(3) = (3)³ − 6(3)² + 9(3) + 1 = 1

Uji turunan kedua

f ”(1) = 6(1) − 12 = −6 < 0

Karena f ”(1) < 0 maka f(1) = 5 adalah nilai balik maksimum

f ”(3) = 6(3) − 12 = 6 > 0

Karena f ”(3) > 0 maka f(3) = 1 adalah nilai balik minimum

Contoh 5

Tentukan jenis ekstrim dari fungsi \(\mathrm{f(x)=x^{4}+1}\)

Jawab :

f ‘(x) = 4x³ 

f ”(x) = 12x² 

f ‘(x) = 0

⇔ 4x³ = 0

⇔ x = 0

Nilai stasioner pada x = 0 :

f(0) = (0)⁴ + 1 = 1

Uji turunan kedua

f ”(0) = 12(0)²  = 0

Karena f ”(0) = 0 maka f(0) belum dapat ditetapkan

Uji turunan pertama

untuk x < 0 diperoleh f ‘(x) < 0 (turun)

untuk x > 0 diperoleh f ‘(x) > 0 (naik)

Karena pada x = 0 terjadi perubahan dari turun menjadi naik, maka f(0) = 1 adalah nilai balik minimum.

Latihan Soal

Latihan 1

Diketahui fungsi \(\mathrm{y=ax^{3}+bx^{2}}\) dengan a dan b konstan. Jika nilai stasioner di \(\mathrm{x=1}\) adalah −1, tentukan nilai a − b !

Jawab :

Substitusi titik stasioner (1, −1) ke fungsi y :

y = ax³ + bx²

⇔ −1 = a(1)³ + b(1)²

⇔ −1 = a + b ……………..(1)

f(x) = ax³ + bx²

f ‘(x) = 3ax² + 2bx

Karena f stasioner di x = 1 maka :

f ‘(1) = 0

⇔ 3a(1)² + 2b(1) = 0

⇔ 3a + 2b = 0 …………….(2)

Eliminasi (1) dan (2)

  a +   b = −1   ×3

3a + 2b = 0     ×1

3a + 3b = −3

3a + 2b = 0   _

          b = −3

Dari persamaan (1)

a + b = −1

a + (−3) = −1

a = 2

Jadi, a − b = 2 − (−3) = 5

Latihan 2

Grafik fungsi kuadrat \(\mathrm{f(x)=-x^{2}-2px+3}\) mencapai nilai balik maksimum untuk absis \(\mathrm{x=-1}\). Tentukan nilai p dan koordinat titik balik maksimum fungsi tersebut !

Jawab :

f(x) = −x² − 2px + 3

f ‘(x) = −2x − 2p

Karena f mencapai nilai balik maksimum di \(\mathrm{x = -1}\) maka :

f ‘(−1) = 0

⇔ −2(−1) − 2p = 0

⇔ 2 − 2p = 0

⇔ p = 1

Untuk p = 1 maka 

f(x) = −x² − 2(1)x + 3

f(x) = −x² − 2x + 3

Nilai balik maksimum :

f(−1) = −(−1)2 − 2(−1) + 3 = 4

Jadi, titik balik maksimum : (−1, 4)

Latihan 3

Fungsi kuadrat \(\mathrm{f(x)=ax^{2}+bx-5}\) mempunyai koordinat titik balik minimum di \(\mathrm{(2,-9)}\). Hitunglah nilai \(\mathrm{a + b}\) !

Jawab :

Substitusi titik (2, −9) ke fungsi f(x)

−9 = a(2)²  + b(2) − 5
4a + 2b = −4 ………………….(1)

f ‘(x) = 2ax + b

Karena f mencapai nilai balik minimum di \(\mathrm{x=2}\), maka :

f ‘(2) = 0

2a(2) + b = 0

4a + b = 0 ……………………..(2)

Eliminasi (1) dan (2) diperoleh 

a = 1

b = −4

Jadi, a + b = 1 + (−4) = −3